
![]()
Тел: +7(391)254-8445
E-mail: rcit@inbox.ru
Статьи
технической тематики из периодических изданий
«Регионального Центра Инновационных Технологий»
Оценка надежности и выбор стратегии
профилактик оборудования тяговых подстанций
с учетом степени износа
Вестник ВНИИЖТ
Е.Е. БАКЕЕВ, А.И. ШАРАПОВА
Оценка надежности и выбор стратегии
профилактик оборудования тяговых подстанций
с учетом степени износа
Существующая система организации испытаний и профилактических ремонтов ориентирована на эксплуатацию оборудования со сроком службы, не превышающим предельно допустимого. В результате аварийность тяговых подстанций с годами возрастает.
Одной из причин является старение оборудования, что подтверждается статистикой на
основе баз данных АСУЭ и КАСАНТ. Актуальной задачей является организация оптимального режима профилактик.
Сложность проблемы заключается в том, что существующие методы
диагностики не дают полной информации о надежности оборудования, поэтому необходимо найти оптимальную стратегию обслуживания при неполной информации о состоянии системы.
В статье рассматривается задача выбора оптимального
режима профилактик оборудования с учетом старения.
Показано, что процесс, описывающий состояния системы, является регенерирующим, и поэтому средние удельные потери при
«бесконечной» неопределенно длительной эксплуатации системы можно определить как отношение средних потерь за
период профилактики к средней длительности этого периода.
Приводится описание алгоритма формирования оптимального плана профилактик.
Для приближенного решения задачи неопределенно длительной эксплуатации системы может быть использована методика УРРАН, разработанная ОАО «НИИАС», которая базируется на составлении карт надежности оборудования.
Эксплуатационная надежность тяговых подстанций существенно зависит от технического состояния их оборудования.
В настоящее время значительная часть оборудования тяговых подстанций имеет сроки службы, превышающие установленные нормативными документами, что необходимо учитывать при формировании планов профилактических и ремонтных работ.
Актуальность задачи очевидна из рассмотрения статистических данных на примере Московской железной дороги (табл. 1).
Как следует из табл. 1, более половины трансформаторов на тяговых подстанциях имеет срок службы больше нормативного 25 лет по ГОСТ 11677 – 85.
Существующая система организации испытаний и профилактических ремонтов ориентирована на эксплуатацию оборудования со сроком службы, не превышающим предельно допустимого. В результате аварийность тяговых подстанций с годами возрастает.
На рис. 1 представлены показатели аварийности тяговых подстанций (ЭЧЭ) сети железной дороги, взятые из базы данных автоматизированной системы управления электроснабжением (АСУЭ).
Надежность оборудования тяговых подстанций определяется степенью износа и старения за время эксплуатации.
Кривые снижения с течением времени надежности трансформаторов и фидерных выключателей приведены на рис. 2.
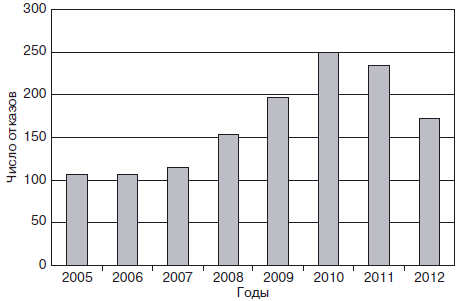
Рис. 1. Отказы тяговых подстанций
Таблица 1. Старение оборудования тяговых подстанций
| Вид оборудования |
Всего на дороге, шт. |
В том числе со сроком службы более 25 лет |
|
|
Количество оборудования, шт./font> |
% | ||
| Выключатели 110 кВ | 559 | 401 | 72 |
| Выключатели 35 кВ | 431 | 325 | 75 |
| Выключатели 6 и 10 кВ | 2040 | 1026 | 50 |
| Выпрямительные агрегаты 3,3 кВ | 353 | 221 | 63 |
| Тяговые трансформаторы | 476 | 167 | 35 |
| Понизительные трансформаторы | 217 | 167 | 77 |
| Трансформаторы СЦБ | 246 | 192 | 78 |
| Трансформаторы собственных нужд тяговых подстанций | 336 | 283 | 84 |
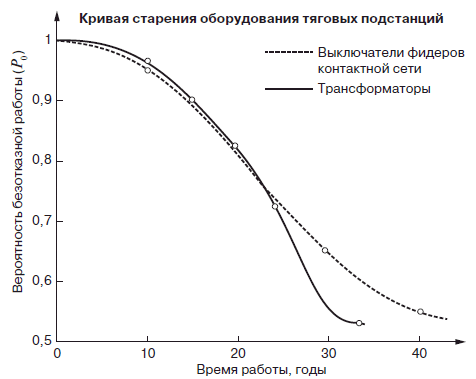
Рис. 2. Снижение вероятности безотказной работы оборудования
тяговых подстанций при длительных сроках эксплуатации
Эти характеристики построены в результате обработки записей отказов из базы данных комплексной автоматизированной системы анализа неисправностей транспорта (КАСАНТ) по Московской железной дороге.
Как видим, после достижения предельного срока 25 лет уровень надежности падает ниже 0,75, что является недопустимо низким.
Эксплуатация такого оборудования строится на основе регулярных профилактических ремонтов, выполняемых через установленные нормативами интервалы времени t0.
На рис. 3 показан принцип продления срока службы оборудования за счет регулярных профилактических ремонтов. Но поскольку после каждого ремонта достичь уровня надежности P0 =1 практически нереально, то со временем огибающая кривая достигает критического значения P, после которого оборудование следует менять на новое.
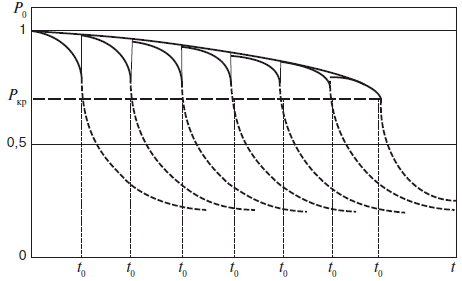
Рис. 3. Обслуживание с регулярными профилактиками
Такая система профилактик позволяет поддерживать в эксплуатации работу изношенного оборудования, но она связана со значительными трудозатратами и удорожает стоимость содержания тяговых подстанций, не позволяя перейти к более экономичным методам их обслуживания.
С учетом изложенного очевидна актуальность изменения системы обслуживания тяговых подстанций.
Сложность проблемы заключается в том, что существующие методы диагностики не дают полной информации о надежности оборудования, поэтому необходимо найти оптимальную стратегию обслуживания при неполной информации о состоянии системы.
Если оборудование имеет возрастающую интенсивность отказов, т. е. является стареющим, то интервалы между профилактиками выбираются из условия
tп << t0,
где tп — период профилактики,
t0 — время наработки на отказ.
Оптимальным будет такой режим, когда моменты профилактик не могут быть указаны заранее, а планируются в моменты времени, когда наработка оборудования с момента последнего включения достигла заданной величины.
Такой режим профилактики иногда называют профилактикой по возрасту или оперативной профилактикой (рис. 4).
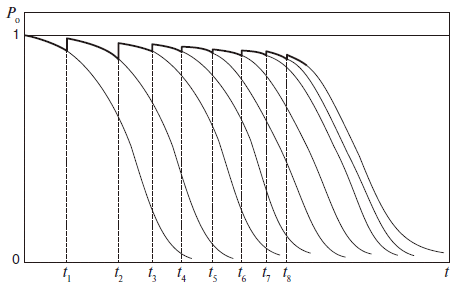
Рис. 4. Интервалы профилактик с учетом старения оборудования
Как показано в [1 – 10], оптимальным будет режим, при котором отказавшее устройство заменяют непосредственно перед моментом отказа, однако для этого необходимо иметь такую систему диагностики, которая позволит точно определять оставшийся ресурс оборудования.
Реально существующая ситуация с диагностикой позволяет иметь лишь относительную оценку ресурса, поэтому выбор оптимальной стратегии обслуживания может быть построен на основе вероятностных оценок.
Теоретическое обоснование решения подобной задачи приведено в [2].
Пусть один из периодов работы оборудования имеет длительность T и на этом интервале планируем n профилактик.
Обозначим среднюю стоимость проведения одной профилактики — c, а среднюю стоимость потерь за единицу времени пребывания оборудования в состоянии отказа — cп.
Если отказ произошел после n-й профилактики, то общая стоимость S эксплуатации оборудования на этом интервале будет равна
S = nc+cпΔt ,
где Δt — время от момента возникновения отказа до выполнения очередной профилактики в момент T.
Обозначим через ξ случайное время до отказа оборудования между профилактиками с номерами и k и k + 1.
Тогда
S (ξ)=(k + 1) c + cп ( xk+1 − ξ)
при
xk < ξ < xk+1;
S(ξ)= nc+cп (T −ξ)
при
xk < ξ < T .
При неопределенно длительной («бесконечной») эксплуатации системы средняя удельная стоимость ее эксплуатации определится следующим образом:
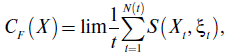
где
N(t) — число циклов профилактики, выполненных к моменту t;
CF (X) зависит от функции распределения F(t) случайной величины ξ;
S (Xi, ξi) — случайное время до отказа системы на интервале
i.
При неполной информации о надежности системы мы полагаем, что нам известно только ее значение в точке T :
где π — квантиль — допустимый уровень вероятности
безотказной работы для распределения случайной
величины ξ на интервале от k = 0 до k = n:
Очевидно, что математические ожидания S и X зависят от F(t).
Процесс, описывающий состояния системы, является регенерирующим, и поэтому средние удельные
потери при «бесконечной» неопределенно длительной эксплуатации системы можно определить как отношение средних потерь за период профилактики к
средней длительности этого периода.
Выбирая оптимальный план профилактик, мы желаем минимизировать значение функции
![]()
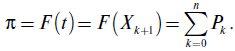
Алгоритм формирования оптимального плана в соответствии с [2] определяется следующим образом:
- введем обозначения
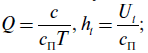
- значение оптимального числа n профилактик на интервале (0, T) определяется численным приближенным решением уравнения
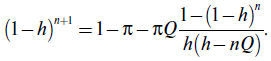
Это уравнение нельзя решить явно относительно h, но для заданной пары значений π и Q можно численными методами получить оптимальное значение n, соответствующее наилучшему плану профилактик.
При изменениях π от 0 до 1 параметр Q выбирается в диапазоне от 0,001 до 0,2. Выполняя рекуррентные расчеты при различных Q и π, определяем оптимальное значение n на расчетном интервале.
Достоверность результатов будет зависеть от объема статистических данных, характеризующих функцию F(t), а следовательно, и
CF (X).Вид функции F(t) может быть определен с использованием методик УРРАН, разработанных ОАО «НИИАС», которые базируются на составлении карт оценки надежности для каждого вида оборудования в зависимости от срока его эксплуатации.
Стоимость эксплуатации оборудования Э может быть определена с учетом расходов на эксплуатацию р и потерь от аварий Р:
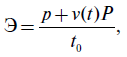
где
v(t) — вероятность отказа на интервале между профилактиками;
t0 — интервал времени между профилактиками.
Выбор интервала профилактики t0 может быть сделан исходя из допустимых расходов на эксплуатацию [11] и уровня надежности оборудования:
![Выбор интервала профилактики t0 может быть сделан исходя из допустимых расходов на эксплуатацию [11] и уровня надежности оборудования](gif/art093-8.gif)
Очевидно, что при частых профилактиках стоимость эксплуатации возрастает, однако, с другой стороны, при этом снижается вероятность отказа v(t), поэтому поиск оптимального режима профилактик является минимаксной задачей.
Организация профилактик оборудования тяговых подстанций с учетом старения и фактического ресурса позволит сократить эксплуатационные расходы без снижения уровня надежности.
2. Б арзилович Е. Ю., Кашт анов В. А. Организация обслуживания при ограниченной информации о надежности системы.
М.: Советское радио, 1975. 135 с.
3. Яхьяев Н. Я., Кораблин А. В. Основы теории надежности.
М.: Академия, 2014. 256 с.
4. Ос трейковский В. А. Теория надежности. М.: Высшая
школа, 2008. 463 с.
5. Грешилов А. А. Математические методы принятия решений. М.: МГТУ им. Н. Э. Баумана, 2006. 584 с.
6. Климов Г. П. Теория массового обслуживания. М.: МГУ,
2011. 312 с.
7. Кофман А., Фор Р. Займемся исследованием операций.
М.: Мир, 1966. 278 с.
8. Кофман А., Крюон Р. Массовое обслуживание. Теория и
приложения. М.: Мир, 1965. 302 с.
9. Риордан Дж. Вероятностные системы обслуживания. М.:
Связь, 1965. 182 с.
10. Barlow R., Proshan F. Planned replacement. Studies in applied
probability and management. Science, Stanford University press,
Stanford 1962, pp. 63 – 87.
11. Crookes P. Replacement strategies. Operational Research Quarterly,
14, № 2, 1963, pp. 167 – 184.
БАКЕЕВ Евгений Евгеньевич,
доцент кафедры «Электроэнергетика железнодорожного
транспорта», ИТТСУ МИИТ.
127994, Москва, ул. Образцова, д. 9, стр. 9.
Тел.: (916) 219-15-60.
E-mail: bakeeve@yandex.ru
ШАРАПОВА Анна Игоревна,
конструктор МЭЗ ДКРЭ ОАО «РЖД»,
ассистент кафедры «Электроэнергетика
железнодорожного транспорта»,
аспирант ИТТСУ МИИТ.
109382, Москва, платформа Депо, д. 6, стр.1.
Тел.: (495) 351‑27‑64.
E-mail: sharap7@mail.ru
Вестник ВНИИЖТ - Е.Е. БАКЕЕВ, А.И. ШАРАПОВА
Оценка надежности и выбор стратегии профилактик оборудования тяговых подстанций с учетом степени износа