ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
ПРОБЛЕМЫ ТРАНСПОРТА ВОСТОЧНОЙ СИБИРИ

Анализ распределения напряжений
в резьбовых соединениях оси колёсной пары
на примере торцевого крепления обоймы подшипника шайбой
А.В. Кулешов, А.А. Кудлацкий, Л.Б. Цвик

   Современный вагон представляет собой сложную статически неопределимую механическую систему, на которую при движении ее по железнодорожному пути с неровностями действуют статические, динамические вертикальные, поперечные и продольные горизонтальные силы, носящие, как правило, вероятностный характер. Болтовые соединения являются неотъемлемой частью различных вагонов и воспринимают эти силы. Это предъявляет особые требования к точности анализа напряженнодеформированного состояния (НДС) болтовых соединений.

   Буксовый узел является одним из важнейших элементов вагона, определяющим безопасность движения. В практике встречаются отказы, связанные с обрывом болтов М12 осей РУ1 и М20 осей РУ1Ш (рис. 1). Основными причинами возникновения обрывов являются: действие горизонтальных сил, вызывающих чрезмерную деформацию резьбы и обрыв стержня болта М20, нарушение технологии монтажа-демонтажа буксового узла и наличие внутренних металлургических дефектов в болтах. Встречается также ослабление крепительной крышки буксового узла, что приводит к попаданию в него влаги. Для расчётного анализа работоспособности рассматриваемого соединения, учитывающего возможность появления перечисленных видов отказов, необходим уточнённый анализ деформаций его элементов в эксплуатационных условиях.

   Одной из применяемых в настоящее время методик расчёта деформаций рассматриваемых соединений является методика, основанная на гипотезе о ступенчатом характере распределения контактных давлений по виткам резьбы (гипотеза Н.Е. Жуковского) [3]. В данной работе представлена методика расчётной оценки деформаций в резьбовых соединениях типа болт-гайка в системе MSC/Nastran, реализующей метод конечных 77 элементов МКЭ. Такой подход требует применения вычислительной техники и позволяет последовательно уточнять используемые модели деформирования. В частности, применение МКЭ позволяет без принципиального усложнения методики учитывать пластический характер деформирования материала, реальную форму элементов болтового соединения и, что существенно, учесть изменяемость контактных напряжений как на поверхности контакта витков резьбы, так и по её виткам с учётом пространственного характера деформирования деталей соединения.

Рис. 1. Повреждения крепёжных болтов буксового узла:
а – обрыв головок болтов М12 крепления стопорной планки в оси РУ1,
б – обрыв головок болтов М20 торцевого крепления подшипников на шейке оси РУ1Ш

   Для оценки достоверности расчетов сравним результаты, полученные с помощью решения уравнений теории упругости для модельного резьбового соединения М10 (т. е. соединения, для которого решение рассматриваемой задачи о распределении усилий по виткам известно), полученным для него И.А. Биргером [3] и основанном на конечно-элементной дискретизации элементов соединения. Для расчета распределения нагрузки между витками резьбы в [3] используется приближённое уравнение относительно функции одной переменной (функции распределения контактных давлений по виткам)

   Уравнение (1) описывает контактное взаимодействие в системе болт-гайка приближённо и не опирается на решение соответствующей контактной задачи, учитывающей возможность проскальзывания и взаимного отставания друг от друга контактирующих поверхностей. При этом q(z) – искомая функция распределения по виткам – приближается «ступенчатой» функцией, в соответствии с чем узловая сила в модели деформировании [3] определяется равенством

   где q_i – контактное давление на i-м витке; r_i – радиус узла; t_i – ширина ступени; k – номер узла конечно-элементной дискретизации в пределах витка.

   Осевая составляющая суммы узловых сил равна внешней силе, действующей на болт

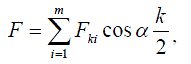(3)

   где α – угол профиля резьбы.

   Контактные давления на i--м витке определяются отношением величины осевой силы F_ki к соответствующей площади «ступеньки» .

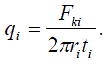(4)

   Опишем теперь результаты КЭ-решения этой же модельной задачи с учётом контактного характера взаимодействия витков резьбы в соединении болт-гайка. Предварительно были построены дискретные конечноэлементные модели деформирования как болта, так и соответствующей гайки. Точность КЭ-приближения обеспечивалась необходимой степенью сгущения КЭ-разбивки. При этом степень измельчения КЭ-разбивки подбиралась из условия сходимости конечно-элементных решений по мере измельчения КЭ-разбивки по закону геометрической прогрессии. Погрешность построенных КЭ-решений не превышала при этом 5 %.

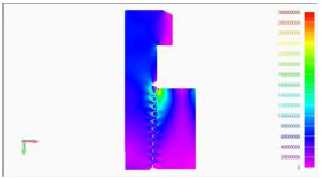
   На рис. 2 показано осесимметричное распределение нормальных напряжений σ_x (ось x – вертикальна) в осевом сечении соединения М10, полученное с помощью МКЭ. На рис. 3 – распределение контактных давлений в осевом сечении поверхности контактного взаимодействия.

Рис. 2. Распределения напряжений в осевом сечении	Рис. 3. Эпюра нормальных напряжений

   Сравнение результатов (см. рис. 4) КЭ-анализа и результатов аналитического моделирования показывает, что полученные с их помощью значения контактных давлений качественно одинаковы, а количественно различаются незначительно. Расхождение объясняется тем, что традиционные расчеты деталей машин ведутся по средним напряжениям в опасных сечениях и с учетом различных экспертных коэффициентов, учитывающих реальные условия работы. Приведённое сопоставление результатов КЭ- моделирования рассмотренной задачи с известным решением, приведённым в [3] показывает его корректность и эффективность в рассматриваемом классе задач.

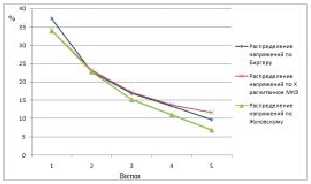
Рис. 4. Сравнение результатов КЭ-анализа с решением [3]

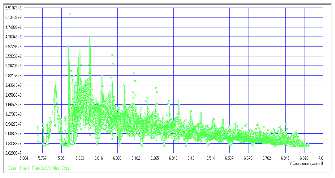
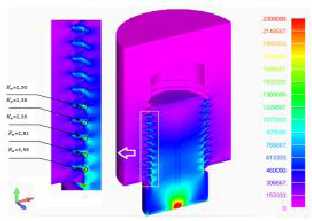
   Опишем теперь применение разработанной уточнённой методики к анализу резьбового соединения элементов оси колёсной пары. В частности, рассмотрим контактное взаимодействие витков резьбы болта М20, фиксирующего положение на торце оси упорной шайбы, препятствующее смещению буксового узла вдоль рассматриваемой оси. При КЭ- моделировании между противоположными (относительно поверхности возможного контакта) узлами разбивки введены контактные элементы типа GAP, усилия в которых появляются только после сближения узлов в направлении перпендикулярном к поверхности контакта [4]. Анализ показывает, что в рассматриваемом болтовом соединении нагрузка на первый виток составляет примерно 16 % от общей величины осевой нагрузки.

   Нагрузка, приходящаяся на второй рабочий виток, в 1,3 раза меньше, чем нагрузка на первый виток. Максимальный коэффициент концентрации напряжений в резьбовом соединении «болт – ось» (рис. 5) имеет место во впадине под первым рабочим витком болта, находящимся в зацеплении с резьбой в оси, и составляет K_σ = 3,5.

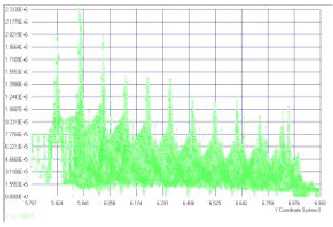
Рис. 5. Распределение нормальных напряжений σx в сечении болта М20	Рис. 6. Распределения контактных давлений по виткам в резьбовом соединении М20

   Концентрация затягивающего усилия на нескольких первых витках стандартной резьбы часто ведёт к срыву или вытягиванию первых витков внутренней резьбы, т. е. к её ослаблению. Под действием циклической эксплуатационной нагрузки в указанных зонах могут локализоваться усталостные трещины. Для увеличения ресурса работоспособности рассматриваемых соединений могут быть использованы специальные профили резьбы. Для сравнительной оценки распределения контактных давлений с помощью разработанной численной методики было осуществлено моделирование деформирование эксплуатационной нагрузкой резьбового соединения типа SELF-LOCK [5]. Характерной особенностью рассматриваемого типа соединений является то, что его болт может использоваться совместно со стандартной наружной резьбой метрического типа. Комбинация стандартной метрической резьбы болта с резьбой гнезда, выполненной по стандарту SELF-LOCK, позволяет использовать данное резьбовое соединение многократно, без срывов или вытягивания первых витков внутренней резьбы, и ослабления в целом резьбового соединения.

   Объясняется это тем, что использование в резьбовом соединении для внутренней резьбы профиля SELF-LOCK позволяет распределять нагрузку более равномерно по всем виткам внутренней резьбы, т. е. на всю её длину [5]. В тех случаях, когда болты подвергаются длительному воздействию переменных нагрузок и вибрации, они могут раскручиваться. Причина этого в том, что во время затяжки болты растягиваются подобно пружине под действием большой нагрузки, и только трение препятствует раскручиванию болтового соединения.

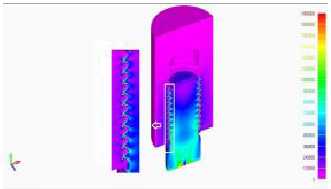
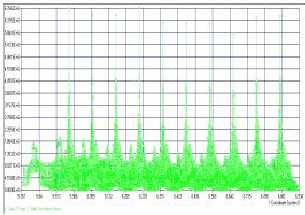
Рис. 7. Эпюра интенсивности напряжений в элементах резьбового соединения М20 типа self-lock	Рис. 8. График распределения контактных давлений по виткам в соединении self-lock
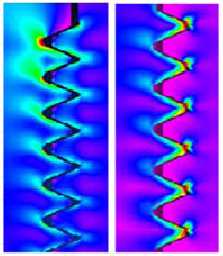	Рис. 9. Сравнение распределения напряжений в стандартной резьбе и в self-lock методом фотоупругости [5]

   Представленные на рис. 7-8 результаты численного анализа, осуществлённого с помощью разработанной методики, а также известные результаты экспериментальных исследований (рис. 9) показывают, что профиль типа SELF-LOCK создаёт более равномерное по виткам резьбы распределение контактных давлений. Таким образом, указанный профиль позволяет более эффективно, чем широко применяемая метрическая резьба, препятствовать как раскручиванию болтового соединения, так и его разрушению.

 БИБЛИОГРАФИЧЕСКИЙ СПИСОК К

   1. Зенкевич О. Метод конечных элементов в технике. – М., 1975.
   2. Биргер И.А. Иосилевич Г. Б. Резьбовые и фланцевые соединения. – М., 1990.
   3. Рычков С.П. Моделирование конструкций в среде Femap with NX Nastran. – М. : ДМК пресс, 2013.
   4. Каталог продукции фирмы FRANKEN GmbH & Co. KG.

ПРОБЛЕМЫ ТРАНСПОРТА ВОСТОЧНОЙ СИБИРИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
 ИРКУТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
Анализ распределения напряжений в резьбовых соединениях оси колёсной пары на примере торцевого крепления обоймы подшипника шайбой
А.В. Кулешов, А.А. Кудлацкий, Л.Б. Цвик
УДК 628.88